Tác giả: Thạc sỹ Phạm Mai Dung
Trường Đại học Công nghiệp Dệt May Hà Nội
Tóm tắt
Tích phân là một trong những nội dung khó, có tính trừu tượng cao. Tuy nhiên, tích phân lại có những ứng dụng rất cụ thể và hiệu quả trong cuộc sống như đo chiều dài của một đường cong, tính diện tích của một hình phẳng, tính diện tích bề mặt và thể tích của một vật thể,....Trong phạm vi bài viết, tác giả xin chỉ ra một số ứng dụng của phép toán tích phân vào ngành Dệt may để người đọc có thể dễ dàng tiếp cận với khái niệm khó và trừu tượng này.
1. Mở đầu
Tích phân là một trong những nội dung chính được giảng dạy trong học phần Toán ứng dụng của sinh viên trường Đại học Công nghiệp Dệt May Hà Nội. Tích phân bao gồm tích phân đơn, tích phân bội, tích phân đường, tích phân mặt đều là những dung khó tiếp cận và ít gây được hứng thú với sinh viên. Tuy nhiên, để tính được chiều dài đường cong, tính diện tích đa giác phức tạp, tính thể tích vật thể phi tiêu chuẩn,…một cách chính xác tuyệt đối, chúng ta chỉ có thể sử dụng một công cụ duy nhất đó chính là phép tính tích phân.
Trong bài viết này, tác giả xin trình bày một số ứng dụng của tích phân để các em sinh viên có thể vận dụng vào ngành học của mình, đồng thời giúp các em thấy được vai trò, ý nghĩa quan trọng của tích phân trong đời sống thực tiễn.
2.Nội dung
Tích phân là một khái niệm toán học. Tích phân cùng với vi phân (differentiation) đóng vai trò là 2 phép tính cơ bản, chủ chốt trong lĩnh vực giải tích (calculus). Có thể hiểu đơn giản tích phân như là diện tích hoặc diện tích tổng quát hóa. Giả sử cần tính diện tích một hình phẳng được giới hạn bởi các đoạn thẳng, ta chỉ việc chia hình đó thành các hình nhỏ đơn giản hơn như hình tam giác, hình vuông, hình thang, hình chữ nhật... Nếu xét một hình phức tạp hơn được giới hạn bởi cả đoạn thẳng lẫn đường cong, ta cũng chia nó thành các hình nhỏ hơn, nhưng sẽ xuất hiện các hình thang cong. Tích phân giúp ta tính được diện tích của các hình thang cong đó.
Cho hàm một số biến thực f(x) xác định trên miền giá trị thực [a, b]. Tích phân xác định (definite integral) từ a đến b của f(x), ký hiệu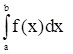 
được định nghĩa là diện tích của một vùng trong không gian phẳng Oxy được giới hạn bởi đồ thị của hàm f(x), trục hoành, và các đường thẳng x = a và x = b, sao cho các vùng trên trục hoành sẽ được tính vào tổng diện tích, còn dưới trục hoành sẽ bị trừ vào tổng diện tích.
Mọi định nghĩa tích phân đều phụ thuộc vào lý thuyết độ đo (measure). Ví dụ, tích phân Riemann dựa trên độ đo Jordan, còn tích phân Lebesgue dựa trên độ đo Lebesgue. Tích phân Riemann là định nghĩa đơn giản nhất của tích phân và thường xuyên được sử dụng trong vật lý và giải tích cơ bản.
2.1. Ứng dụng của tích phân trong việc đo chiều dài
Để đo chiều dài của một cung đường, ta có thể dùng tích phân đơn hặc tích phân đường loại một bằng các công thức sau:
Trong lĩnh vực may mặc, việc đo đạc chính xác chiều dài của một đường cong như đường cổ áo, nách áo, đường đũng quần.... là rất quan trọng để có thể lắp ghép các chi tiết như viền cổ, tra tay áo vào thân áo, ghép đũng trước và đũng sau... một cách ăn khớp, đảm bảo tính thẩm mỹ, tiết kiệm nguyên phụ liệu nhất là khi may trên dây chuyền với số lượng lớn. Để giải quyết vấn đề này, chúng ta có thể tính toán chính xác chiều dài của các đường cong trên mẫu ban đầu bằng ứng dụng của tích phân, rồi tiến hành cắt, ráp mẫu với số lượng lớn.
Ví dụ 1: Để viền cổ áo đẹp, không bị bai dão hay dúm, chúng ta cần phải tính chính xác được chiều dài đường cổ áo.
Mẫu cổ áo hình tim có hình dạng của parabol. Ví dụ khi hạ cổ áo hình tim với chiều cao là 16cm, chiều rộng là 4cm thì đường cổ áo chính là parabol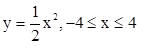 
với đơn vị hệ Oxy trục là cm.
Để viền cổ chiếc áo này, ta sẽ tính chiều dài cung đường cổ áo từ điểm A tới điểm B.
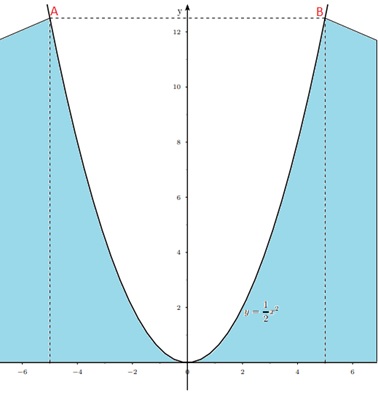
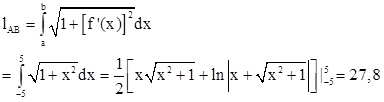
Vậy chiều dài cổ áo xấp xỉ bằng 27,8 cm.
Tương tự, ta có thể tính được chiều dài cổ áo các dạng khác bằng các bước sau:
Bước 1: Xác định đường cổ áo. Với áo cổ tim đường cổ là Parabol, cổ tròn là nửa dưới đường tròn, cổ elip là nửa dưới đường elip,….
Bước 2: Dùng một trong hai công thức ở trên để tính chiều dài đường cổ áo.
2.2. Ứng dụng của tích phân trong việc tính diện tích
Trong thực tiễn cuộc sống cũng như trong khoa học kĩ thuật, người ta cần phải tính diện tích của những hình phẳng cũng như diện tích xung quanh của những vật thể phức tạp. Chẳng hạn khi xây dựng một nhà máy thủy điện, để tính lưu lượng của dòng sông ta phải tính diện tích thiết diện ngang của dòng sông. Thiết diện đó thường là một hình khá phức tạp. Trong may mặc cũng vậy, việc tính chính xác được diện tích một sản phẩm hay một chi tiết giúp chúng ta ước lượng được số mét vải cần sử dụng, từ đó tiết kiệm được chi phí sảnxuất.
Trước khi phép tính tích phân ra đời, với mỗi hình và mỗi vật thể như vậy người ta lại phải nghĩ ra một cách để tính. Sự ra đời của tích phân cho chúng ta một phương pháp tổng quát để giải hàng loạt những bài toán tính diện tích và thể tích nói trên.
Để tính diện tích hình phẳng, ta sử dụng tích phân đơn hoặc tích phân bội 2.
Ví dụ 2: Chiếc dù lớn cho hội nghị ngoài trời có dạng mái tròn vòm cong với bán kính là 4m và chiều cao từ mặt phẳng chứa bán kính tới đỉnh dù là 2m.
Ta có thể coi chiếc dù là vật thể tròn xoay được tạo bởi hình phẳng giới hạn bởi các đường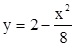 
và y=0 quay quanh trục Oy với đơn vị hệ trục Oxy là mét.
a) Tính diện tích hình phẳng trên.
b) Tính diện tích vải cần thiết để may một chiếc dù.
b) Diện tích xung quanh của chiếc dù khi quay nửa phải hình phẳng quanh trục Oy là:
Vậy diện tích vải cần thiết để may chiếc dù là 61,3m2.
Như vậy, để tính được diện tích hình phẳng hay diện tích xung quanh của vật thể tròn xoay ta cần tiến hành theo các bước sau:
Bước 1: Đối với hình phẳng, ta cần phân tích hình dạng của nó, 2 cận trái phải, đường trên, đường dưới giới hạn hình phẳng. Đối với vật thể, ta cần xác định nó được tạo bởi hình phẳng nào, cận trên, cận dưới, đường cong giới hạn khi quay quanh trục Oy.
Bước 2: Sử dụng các công thức ở trên để tính.
2.3. Ứng dụng của tích phân trong việc tính thể tích
Thể tích là gì? Có thể hiểu một cách đơn giản, thể tích của một vật thể là lượng không gian mà vật đó chiếm. Để tính thể tích, ta sử dụng tích phân đơn, bội 2 hoặc bội 3.
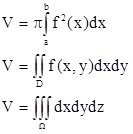
Việc tính thể tích có rất nhiều ý nghĩa trong cuộc sống, minh họa như ví dụ dưới đây.
Ví dụ 3: Một chiếc kinh khí cầu có hình dạng được tạo bởi nửa trên mặt cầu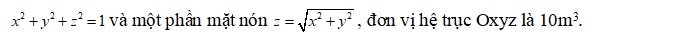 
Người ta dùng kinh khí cầu để vận chuyển người hoặc hàng hóa dưới khoang chứa. Để biết trọng lượng mà kinh khí cầu có thể chở, chúng ta cần tính được thể tích không khí chứa trong kinh khí cầu.
Vậy thể tích không khí trong chiếc kinh khí cầu là 3,9m3.
Việc tính toán lượng không khí chứa trong chiếc kinh khí cầu sẽ giúp chúng ta tính được lực cản không khí, từ đó tính được trọng lượng tối đa mà chiếc kinh khí cầu có thể mang để đảm bảo người và hang hóa trong khoang chứa được an toàn.
3. Kết luận
Qua một số ví dụ trên ta nhận thấy, tích phân có nhiều ứng dụng gần gũi trong đời sống. Chúng ta có thể áp dụng tích phân để tính chiều dài, diện tích, thể tích các vật thể phức tạp. Thông qua các ví dụ trên tác giả muốn kích thích trí tò mò, ham học hỏi của sinh viên đối với khái niệm tích phân và các nội dung khác của học phần Toán ứng dụng. Toán học, tích phân không hề xa lạ, không phải học chỉ để biết mà học để áp dụng vào công việc và cuộc sống hàng ngày.
Tài liệu tham khảo
-
Nguyễn Đình Trí (chủ biên), Tạ Văn Đĩnh, Nguyễn Hồ Quỳnh (2007),Toán học cao cấp tập 1, Nhà xuất bản giáo dục.
-
Nguyễn Hữu Thành,Phạm Mai Dung (2015), Giáo trình Toán ứng dụng, Trường Đại học Công nghiệp Dệt May Hà Nội.